± The Work of a Force

Learning Goal:

To be able to calculate the work done by a force.

If an external force, F, acts on a rigid body, the work, UF, done by the force when it moves along a path s is defined as

UF=∫rF⋅dr=∫sFcosθds

where θ is the angle between the force and the object's direction of motion and r is the position vector that points to the object as it moves along path s.

 

 

 

Part A

Which of the following forces do work?

Check all that apply.

• The frictional force on a crate that is being pushed across a flat floor.
• The weight of a ball that rolls, without slipping, down a ramp.
• A stretched spring that is allowed to contract.
• A compressed spring that is allowed to expand.
• The frictional force on a crate sliding down a ramp

Part B

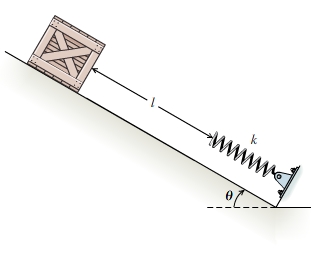
A crate of mass m = 54.0 kg slides a distance l = 4.60 m down a ramp at an angle θ = 25.0 ∘. At the bottom of the ramp is a spring that has a spring constant k = 680 N/m . (Figure 1) What is s, the distance the spring will compress when the crate comes to rest? The ramp is smooth enough that the friction is negligible.

Express your answer numerically in meters to three significant figures.

s =

2.10

m

 

 

 

 

Part C

When a satellite is launched, its orbital radius is usually determined far in advance because the amount of energy required to change its orbit is large. How much work, W, would a rocket thruster on a satellite of mass m = 610 kg need to do to change the satellite's orbital radius from r1 = 2.84×10⁷ m to r2 = 4.16×10⁷ m ? (Figure 2) The Earth's radius is RE = 6.37×10⁶ m . Assume that both orbits are circular.

Express your answer numerically in joules to three significant figures.

W =

2.71×109

J