Absolute Motion Analysis

Learning Goal:

To be able to develop an equation relating the linear distance between moving bodies to the angular position and velocity of the first or driving body and to use this relationship to derive the function for absolute velocity and acceleration of the second body.

A circular cam is in contact with a rectangular lifter and used to intermittently operate a piece of equipment at the end of a lifter arm. The lifter is in contact with the highest point of the cam at the instant shown and the lifter is constrained to move only in the vertical direction. The cam has a radius of

r = 4.2 in and is rotating about point O, which is offset from the center by a distance c = 2.0 in . The cam’s angular position is measured from the positive x axis and is positive clockwise. The angular velocity and acceleration are positive clockwise.

 

 

 

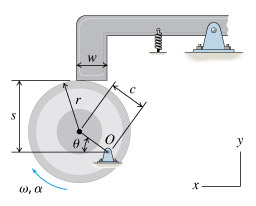
Part A - Velocity of the lifter

Find the linear velocity of the lifter with respect to point O when the cam has an angular position of θ = 31 ∘ and is rotating with an angular velocity of ω = 3.0 rad/s .

Express your answer to two significant figures and include the appropriate units.

v=

5.14 ins

 

Part B - Acceleration of the lifter

Find the linear acceleration of the lifter with respect to point O when the angle is θ = 31 ∘ , the angular velocity is ω = 3.0 rad/s , and the angular acceleration is α = -3.0 rad/s2 .

Express your answer to two significant figures and include the appropriate units. Enter positive value if the acceleration is upward and negative value if the acceleration is downward.

a=	-14.4 ins2

 

Part C - Range of θ for which the position equation is valid

Find the range of θ for which the position equation s=r+csin(θ) is valid if the width of the lifter is w = 1.98 in and its right edge is aligned with O. Give only the range values that lie between 0∘ and 180∘.

Express your answers in degrees, separated by a comma, to two significant figures.

θmin, θmax =

8.1,90

∘