Relative-Motion Analysis: Velocity

Learning Goal:

To understand how to use the relative position and velocity equations to find the linear and angular velocity of members in an assembly.

A piston is driven by a crankshaft as shown. The crank arm

(member AB) has a length of r1=0.60 in and the connecting rod (member BC) has a length of r2=4.65 in . The crankshaft rotates in the counterclockwise or positive direction.

 

 

 

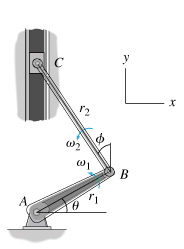
Part A - Relative Motion

The relative velocity equation accounts for the general plane motion of a point on a body. This general plane motion can be broken down into the two primary components of motion, translation and rotation. For the velocity equation, vC=vB+vC/B identify the correct translation and rotation components.

Select the correct answer.

 

Translation:Rotation:vBω2×rC/B

 

 

Part B - Velocity of B

Find the velocity of B, vB, when θ=18.0∘ and ϕ=7.05∘ . The crank is rotating at 300 rpm (revolutions per minute). Express your answer in component form.

Enter the x and y components of the velocity separated by a comma, to three significant figures in in/s.

vB=

-5.82,17.9

i, j in/s

 

 

Part C - Velocity of C

Find the magnitude of the velocity of C, vC, when the piston has moved to the new position θ=30.0∘ and ϕ=6.42∘ . The crankshaft (member AB) is still rotating at 300 rpm .

Express your answer to three significant figures and include the appropriate units.

vC=

17.4 ins

 

 

Part D - Rotational Speed of the Crankshaft

The velocity of the piston is vC=70.0 in/s j the instant when θ=39.0∘ and ϕ=5.76∘ . Find the rotational speed of the crankshaft (member AB) at this instant. The crankshaft is rotating in the counterclockwise or positive direction. (Figure 2)

Express your answer to three significant figures in revolutions per minute.

ω1=

1330

rpm