Equations of Motion: Translation

Learning Goal:

To use the equations of motion as they relate to linear translation of an object to determine characteristics about its motion.

The car shown has a mass of

m=1100 kg and a center of mass located at G. The coefficient of static friction between the wheels and the road is μs=0.250. The dimensions are a=1.25 m, b=1.75 m, and c=0.350 m. Assume the car starts from rest, the wheels do not slip on the road, and that the car experiences constant acceleration. Neglect the mass of the wheels.

 

 

 

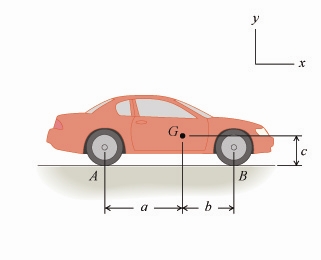
Part A - Shortest Time to Reach a Given Speed with Rear-Wheel Drive

Determine the shortest time it takes the car to reach a speed of v=82.0 km/h , starting from rest, if the engine drives only the rear wheels.

Express your answer to three significant figures and include the appropriate units.

t=

15.5 s

 

 

Part B - Shortest Time to Reach a Given Speed with Front-Wheel Drive

Determine the shortest time it takes the car to reach a speed of v=82.0 km/h, starting from rest, if the engine drives only the front wheels.

Express your answer to three significant figures and include the appropriate units.

t=

22.9 s

 

 

Part C - Shortest Time to Reach a Given Speed with All-Wheel Drive

Determine the shortest time it takes the car to reach a speed of v=82.0 km/h, starting from rest, if the engine drives all four wheels.

Express your answer to three significant figures and include the appropriate units.

t=

9.29 s