Kinetic Energy
Learning Goal:
To
understand the kinetic energy of a rigid body undergoing translational
motion, rotation about a fixed axis, or general motion in the plane.
Consider the rigid body shown in the figure.
Ti=12(dm)v2i .
The kinetic energy of the entire body is found by summing similar
equations for each particle in the body. As the number of particles
increases, by letting the size of each particle go to an infinitesimally
small volume, the sum becomes an integral and the kinetic energy of the
body is
T=12∫mdmv2i .
T=12mv2P−(vP)xωy¯m+(vP)yωx¯m+12IPω2
T=12mv2G+12IGω2 .
The first term of this equation expresses the translational kinetic
energy of the body while the second term expresses the body's
rotational kinetic energy about the mass center.
T=12IICω2 ,
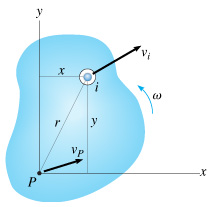
(Figure 1)
An arbitrary ith particle of the body, having mass dm , is located a distance r from an arbitrary point P in the inertial x -y reference plane. If, at the instant shown, the particle has a velocity vi , then the particle's kinetic energy is
When the body is rotating, it is convenient to express the kinetic energy of the body in terms of the velocity of P . Some mathematical manipulation yields:
where x¯ and y¯ are the horizontal and vertical distances, respectively, from P to the mass center of the body, G . In the special case when P coincides with G , the kinetic energy of the body is
In the special case when P coincides with the instantaneous center of zero velocity, the expression for the kinetic energy of the body reduces to
where IIC is the moment of inertia of the body about its instantaneous center of zero velocity.
Because energy is a scalar quantity, the total kinetic energy for a
system of connected rigid bodies is the sum of the kinetic energies of
all its moving parts.
Part A - Kinetic Energy of a Pulley and Weight System
Consider the pulley and weight system shown in the figure. (Figure 2)
The pulley has mass
14.0 kg , outer radius
Ro=250 mm , inner radius
Ri=200 mm , and radius of gyration
kO=231 mm . Cylinder A weighs
53.0 N . Assume there is no friction between the pulley and its axle and that the rope is massless.
At the instant when
ω=69.0 rad/s
clockwise, what is the kinetic energy of the system?
|
|
2290
|
Part B - Kinetic Energy of a Rolling Bicycle Wheel
The bicycle wheel shown in the figure rolls without slipping.
(Figure 3)
The wheel has a weight of
5.30 lb , a radius of
r=12.0 in , and is rolling in such a way that the center hub, O , is moving to the right at a constant speed of
v=14.0 ft/s . Assume all the mass is evenly distributed at the outer radius r of the wheel/tire assembly.
What is the total kinetic energy of the bicycle wheel?|
|
32.3
|
No comments:
Post a Comment