Equations of Motion: Translation

Learning Goal:

To apply the kinetic equations of motion to rigid bodies undergoing translation.

When a rigid body undergoes translation, each particle of the body has the same acceleration aG=a, where aG is the acceleration of the center of mass. Also, the rotational equation of motion reduces to ∑MG=0. The scalar equations of motion for rectilinear translation, where all particles travel in parallel straight-line paths, become

∑Fx=m(aG)x

∑Fy=m(aG)y

∑MG=0

where ∑Fx and ∑Fy are the sum of the forces in the x and y directions, respectively, m is the mass, and ∑MG is the sum of the moments about the center of gravity. The scalar equations of motion for curvilinear translation, where all particles travel in parallel curved paths, become

∑Fn=m(aG)n

∑Ft=m(aG)t

∑MG=0

where the subscripts n and t denote the normal and tangential directions of motion, respectively. The moment equation for both types of translation, ∑MG=0, can be replaced by a summation of moments about an arbitrary point A, where the moment of maG must be accounted for with the following equation:

∑MA=∑(Mk)A

where the term ∑(Mk)A is the moment of maG about point A. 

 

 

 

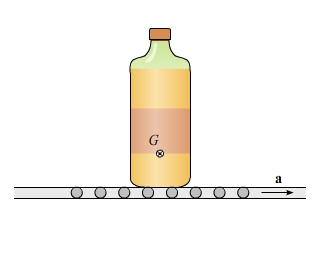
Part A

The bottle in the figure rides on a conveyor belt. (Figure 1) If the belt's acceleration is a = 7.30 ft/s2 , determine the minimum coefficient of static friction that prevents the bottle from slipping. Assume that the bottle is wide enough that it will slip on the belt without tipping.

Express your answer numerically to three significant figures.

μs =

0.227

 

 

Part B

The door in the figure has height c = 3.00 m , mass m = 9.10 kg , and center of gravity G, where b = 1.50 m and d = 1.50 m . (Figure 2) If the man exerts a force F = 10.6 N at h = 1.00 m off the ground, determine the amount of time, t, it takes the man to move the door a distance s = 3.70 m to the right. The door is initially at rest; the initial velocity and position are v0 = 0.000 m/s and s0 = 0.000 m , respectively.

Express your answer numerically in seconds to three significant figures.

t =

2.52

s

Part C

Consider the same door shown in Part B. The distance of d = 1.50 m is the distance from the center of the door to the wheels at points A and B. Find Ay and By, the reaction forces at points A and B, respectively.

Express your answers numerically in newtons to three significant figures separated by a comma.

Ay, By =

46.4,42.9

N