± The Work of a Couple

Learning Goal:

To be able to calculate the work done by a couple on a rigid body.

When a body subjected to a couple moment, M, undergoes general planar motion, the two couple forces do work only when the body undergoes a rotation. When the body rotates in the plane through a finite angle θ (measured in radians) from θ1 to θ2, the work of a couple is

UM=∫θ2θ1Mdθ

If the couple moment, M, has a constant magnitude, then the work is reduced to UM=M(θ2−θ1)

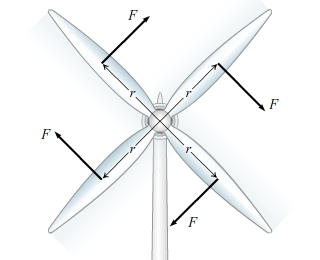
Part A

Each blade on a wind turbine is engineered to produce an effective force through its center of mass that is perpendicular to its long axis. (Figure 1) The magnitude of the force produced by each blade in a wind of speed v is F=(40.0 kg/s)v. If the center of mass of each blade is r = 12.4 m , what is U1, the total work done by the wind turbine's blades, in a wind of speed v = 8.50 m/s after 10 revolutions?

Express your answer numerically in joules to three significant figures.

U1 =

1.06×106

J

Part B

A brake system is tested by rotating a tire and measuring the number of rotations required for the brake system to bring the tire to a stop. (Figure 2) The tire's radius is R = 50.0 cm and the brake system's radius is r = 17.9 cm . A moment of M = 16.9 N⋅m is applied to the tire for 5 rotations before the brake system is applied. The brake system is composed of two pads that are pushed out against the drum with a force that increases as the tire rotates and is described by F=(10.0θ) N. If the coefficient of kinetic friction between the brake pads and the outer ring of the brake system is μk = 0.550, how many rotations, n, will the tire go through before coming to a stop?

Express your answer numerically to three significant figures.

n =

3.70